In this tutorial, I show step by step how to build a simple console appication (reading from the standard input std::cin and writing to the stadard output std::cout) that is using the AbcPMM TraversalSpecificaton-class to calculate the log-likelihood of the PMM model on a given tree, trait-data and model parameters. The code for this example is available from the following directory in the SPLITT github repository:
The TraversalTask template class
Once defined, the TraversalSpecification-class is passed as a template argument to a TraversalTask. This is a template class, which is already written, so the only thing we do is to specify it for our TraversalTask using a typedef like the following one:
typedef TraversalTask< AbcPMM<OrderedTree<std::string, double>> > ParallelPruningAbcPMM;The above code demonstrates one of the powers of C++ templates, namely to define complex types with a single line of code. To understand it, we could write an equivalent but more explicit code:
// use OrderedTree with string-nodes and double branch lengths
typedef OrderedTree<std::string, double> MyTreeType;
// concretise our TraversalSpecification-class
typedef AbcPMM<MyTreeType> MyTraversalSpecificationType;
// and the TraversalTask is:
typedef TraversalTask< MyTraversalSpecificationType > ParallelPruningAbcPMM;An example console application
The next step is to write a program that executes our TraversalTask. For the PMM-example, we will write a program that reads a tree and trait-data from the standard input, than executes a loop reading model parameters from the standard input and calculating log-likelihood of the PMM for these parameters and the input tree and data. Let’s go steb by step through the code for this program.
Reading the input tree
We specify the input tree with the following format:
- The first line of input contains two integers: the number of nodes, \(M\), and the number of tips, \(N\);
- Each one of the next \(M-1\) lines specifies one branch in the form of two words and a real number separated by spaces. The first word is the name of a daughter node, the second word is the name of its parent node, and the real number is the branch length.
Here is an example of an input:
9 5
bonobo ancestor2 4.1
coalla ancestor3 5
gorilla ancestor1 2.8
dolfin ancestor1 3
human ancestor3 4
ancestor1 ancestor2 4.2
ancestor3 root 6
ancestor2 root 4.5Here is the C++ code for reading the tree in the above format from the standard input stream (std::cin):
using namespace PMMUsingSPLITT;
using namespace SPLITT;
using namespace std;
int main(int argc, char* argv[]) {
cout<<"Hello from the SPLITT PMM example!"<<endl;
cout<<"Reading the input tree..."<<endl;
// Read the number of nodes and tips
uint M, N;
cin>>M>>N;
// read the tree
vector<string> daughters(M-1);
vector<string> parents(M-1);
vec t(M-1);
for(int i=0; i < M-1; i++) {
cin>>daughters[i]>>parents[i]>>t[i];
}
// Other code discussed later on...
return 0
}A note on other tree formats
At present SPLITT does not provide functions for parsing different tree formats. I did not need this functionality, because I was using another software to read my input trees and it was very easy to use that software to convert these trees to a list of branches as above. In particular, I’ve used the R-package ape, which can parse many tree-formats. For example, here is how one can specify the above example tree in newick format and parse it using ape:
library(ape)
newick_text <- "((bonobo:4.1,(gorilla:5,dolfin:3)ancestor1:4.2)ancestor2:4.5,(human:4,coalla:5)ancestor3:6)root;"
tree <- read.tree(text = newick_text)Then, one can write the following R-function to print the branches of the tree as above:
PrintBranches <- function(phy) {
M <- length(phy$edge.length) + 1
N <- length(phy$tip.label)
cat(M, " ", N, "\n")
if(!is.null(phy$node.label)) {
labs <- c(phy$tip.label, phy$node.label)
} else {
labs <- c(phy$tip.label, "root", paste0("ancestor", 1:(M - N - 1)))
}
for(i in 1:(M - 1)) {
cat(labs[phy$edge[i, 2]], " ", labs[phy$edge[i, 1]], " ", phy$edge.length[i], "\n")
}
}
PrintBranches(tree)## 9 5
## ancestor2 root 4.5
## bonobo ancestor2 4.1
## ancestor1 ancestor2 4.2
## gorilla ancestor1 5
## dolfin ancestor1 3
## ancestor3 root 6
## human ancestor3 4
## coalla ancestor3 5Great that you are still reading! As a visual reward, here is how the example tree looks like (note that this tree does not reflect the true ancestral relationship between the mentioned species):
plot(tree)
edgelabels(text = tree$edge.length)
nodelabels(text=tree$node.label)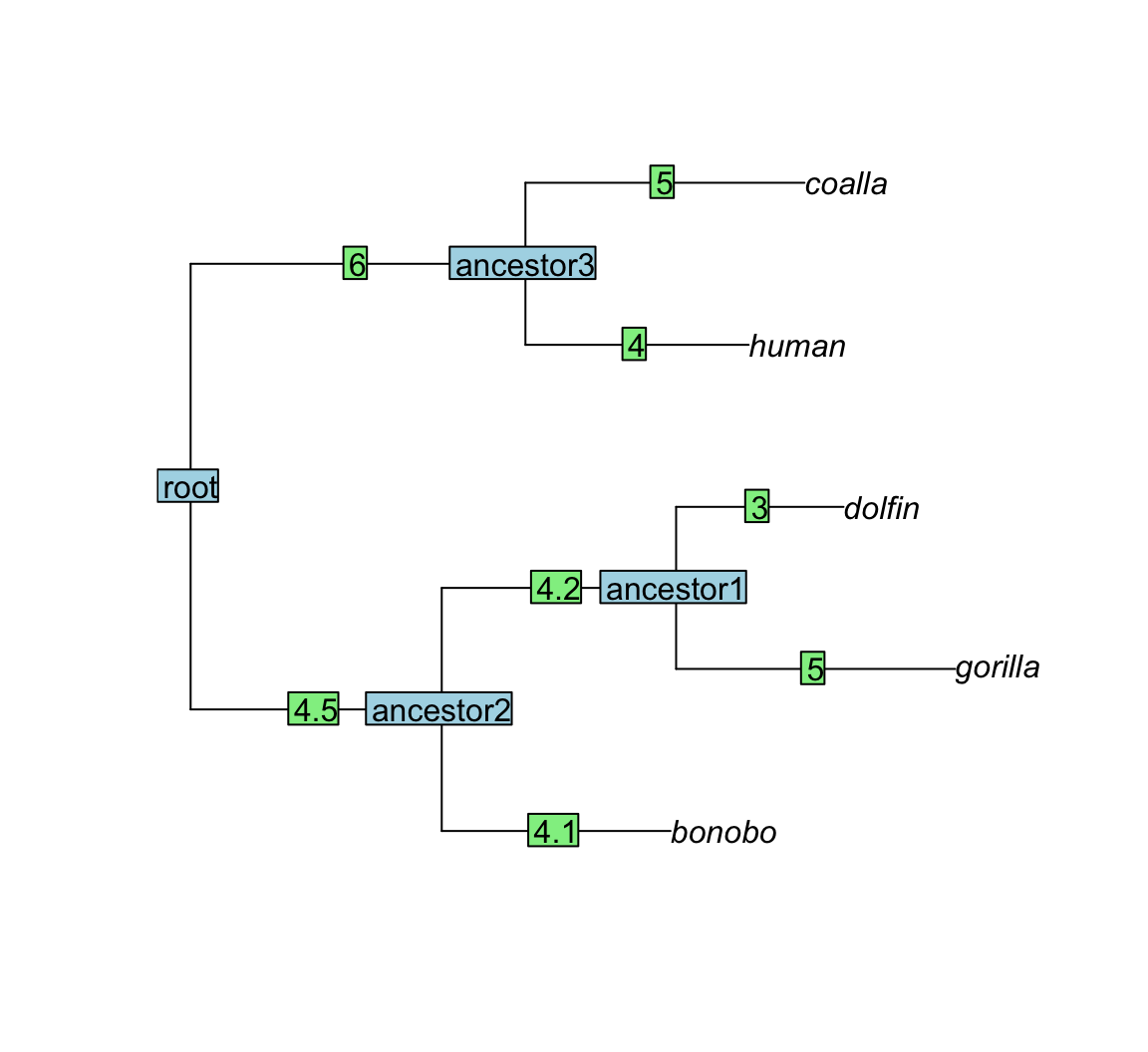
Reading the trait data
After reading the tree, the next step is to read the trait-values associated with each of the \(N\) tips in the tree. Each of the next \(N\) lines contains a tip-name and the corresponding trait values separated by a space. Here is how we read this data in the C++ program:
using namespace std;
int main(int argc, char* argv[]) {
// previously discussed code
cout<<"Reading the trait data..."<<endl;
vector<string> tip_names(N);
vec x(N);
for(int i = 0; i < N; i++) {
cin>>tip_names[i]>>x[i];
}
// other code discussed later
return 0;
}Then, we create a ParallelPruningAbcPMM::DataType object by calling its constructor. If you don’t remember how we defined ParallelPruningAbcPMM::DataType, just look back in the Writing a traversal specification-manual).
using namespace std;
int main(int argc, char* argv[]) {
// previously discussed code
// create the data-object
typename ParallelPruningAbcPMM::DataType data(tip_names, x);
// other code discussed later
return 0;
}
Creating the TraversalTask object
Now everything is set up to create a ParallelPruningAbcPMM object. We do this by calling its constructor, which receives four arguments:
-
branch_start_nodes- this is anstd::vector< NodeType > const&denoting the parent-node in each branch in the tree; -
branch_end_nodes- this is anstd::vector< NodeType > const&denoting the daughter-node in each branch in the tree, corresponding tobranch_start_nodes; -
lengths- this is anstd::vector< LengthType > const&denoting the length of each branch in the tree, corresponding tobranch_start_nodes; -
input_data- this is aDataType const&denoting the input data object for this traversal task.
Calling the ParallelPruningAbcPMM constructor triggers the creation of the internal objects of the framework, i.e. an OrderedTree object maintaining the order in which the nodes are processed and a PreOrderTraversal or a PostOrderTraversal object implementing different parallelization modes of the two traversal types.
Here is how we construct the object in the example program:
using namespace std;
int main(int argc, char* argv[]) {
// previously discussed code
// Create the TraversalTask object: this will create the OrderedTree and the
// AbcPMM objects in the memory.
ParallelPruningAbcPMM pruningTask(parents, daughters, t, data);
// other code discussed later
return 0;
}The main loop
In the main loop of the program, we read PMM-parameters \(\mathbf{\Theta}=<g_{M}, \sigma, \sigma_{e}>\) from the standard input and calculate the PMM log-likelihood for these parameters and the input tree and data. To calculate the log-likelihood, first we call the TraverseTree method of our pruningTask object to calculate the coefficients \(a_{M}\), \(b_{M}\) and \(c_{M}\) for the parameters \(\sigma\) and \(\sigma_{e}\), then we evaluate the log-likelihood value by applying the formula:
\[\ell\ell(\mathbf{\Theta})=a_{M}g_{M}^2+b_{M}g_{M}+c_{M}\].
The TraverseTree method has two arguments:
-
par- this is aParameterType const&. If you don’t remember how we definedParallelPruningAbcPMM::ParameterType, just look back in the Writing a traversal specification-manual). -
mode- this is anuintspecifying the whether SPLITT should performe the traversal using multiple cores and what parallelization order should be applied. This is a more technical topic covered in a separate guide. For now, it is sufficient to know that specifying0for this value tells SPLITT to run in modeAUTO. In this mode, SPLITT will try several modes during the first severalTraverseTreecalls and will stick to the one that resulted in fastest execution for the remaining executions. In the ideal use-case, theTraversalTask’sTraverseTree()method will be called repeatedly, varying the model parameters, the input data and branch lengths on a fixed tree topology. This encompasses all scenarios where a model is fitted to a fixed tree and data, e.g. ML or Bayesian PCM inference.
Here is the corresponding C++ code for reading the main loop:
using namespace std;
int main(int argc, char* argv[]) {
// previously discussed code
// model parameters
double gM, sigma, sigmae;
vec param(2);
cout<<"Main loop..."<<endl;
// run this loop as long as parameters can be read from the standard input
while( cin>>gM>>sigma>>sigmae ) {
param[0] = sigma*sigma;
param[1] = sigmae*sigmae;
cout<<" Calculating a, b, c at the root for sigma="<<sigma<<" and sigmae="<<sigmae<<std::endl;
vec abc = pruningTask.TraverseTree(param, 0);
cout<<" a="<<abc[0]<<", b="<<abc[1]<<", c="<<abc[2]<<std::endl;
double LL = abc[0]*gM*gM + abc[1]*gM + abc[2];
cout<<" LL(gM="<<gM<<", sigma="<<sigma<<", sigmae="<<sigmae<<"): "<<LL<<endl;
}
cout<<"Main loop done."<<endl;
std::cout<<"Good bye!"<<std::endl;
return 0;
}Compiling the program
To compile the program we execute the following command from the directory PMMUsingSPLITT-console-app:
# Feel free to replace the name of the executable with your C++ compiler
clang++ -Wall -O2 -fopenmp -stdlib=libc++ -L/usr/local/lib -L/Library/Frameworks/R.framework/Resources/lib -o PMMLogLikelihood PMMLogLikelihood.cppThis will compile and link the file PMMLogLikelihood.cpp into an executable file called “PMMLogLikelihood”. If the compilation runs fine you should see no error messages.
Testing the program
If the compilation was successful, type the following command.
./PMMLogLikelihood <input.txtWith the exceptino of the line starting with "OpenMP-version:", the above command should produce the following output:
Hello from the SPLITT PMM example!
Reading the input tree...
Reading the trait data...
OpenMP-version: 201107
Main loop...
Calculating a, b, c at the root for sigma=0.5 and sigmae=1
a=-0.432535, b=0.630659, c=-8.21595
LL(gM=0.1, sigma=0.5, sigmae=1): -8.15721
Calculating a, b, c at the root for sigma=0.8 and sigmae=0.4
a=-0.205491, b=0.285864, c=-9.09873
LL(gM=1.5, sigma=0.8, sigmae=0.4): -9.13229
Main loop done.
Good bye!If the OpenMP-version is equal to 0, then, most likely your compiler does not support OpenMP and the header “omp.h” was not available during compilation. If the OpenMP-version was a different number, then your compiler has an other Open MP version in it. If there have been other differences, e.g. the reported values for a, b and c are different, then there could be a problem, which I am not aware of. Please, report this in the SPLITT issues list.
Next steps
The next steps depend on your desired application. If your goal is to call SPLITT from an R-package, you are lucky, because I’ve already done this many times and I have described how to do this in this guide. Otherwise, if you need help, you can ask a question in the SPLITT issues list.