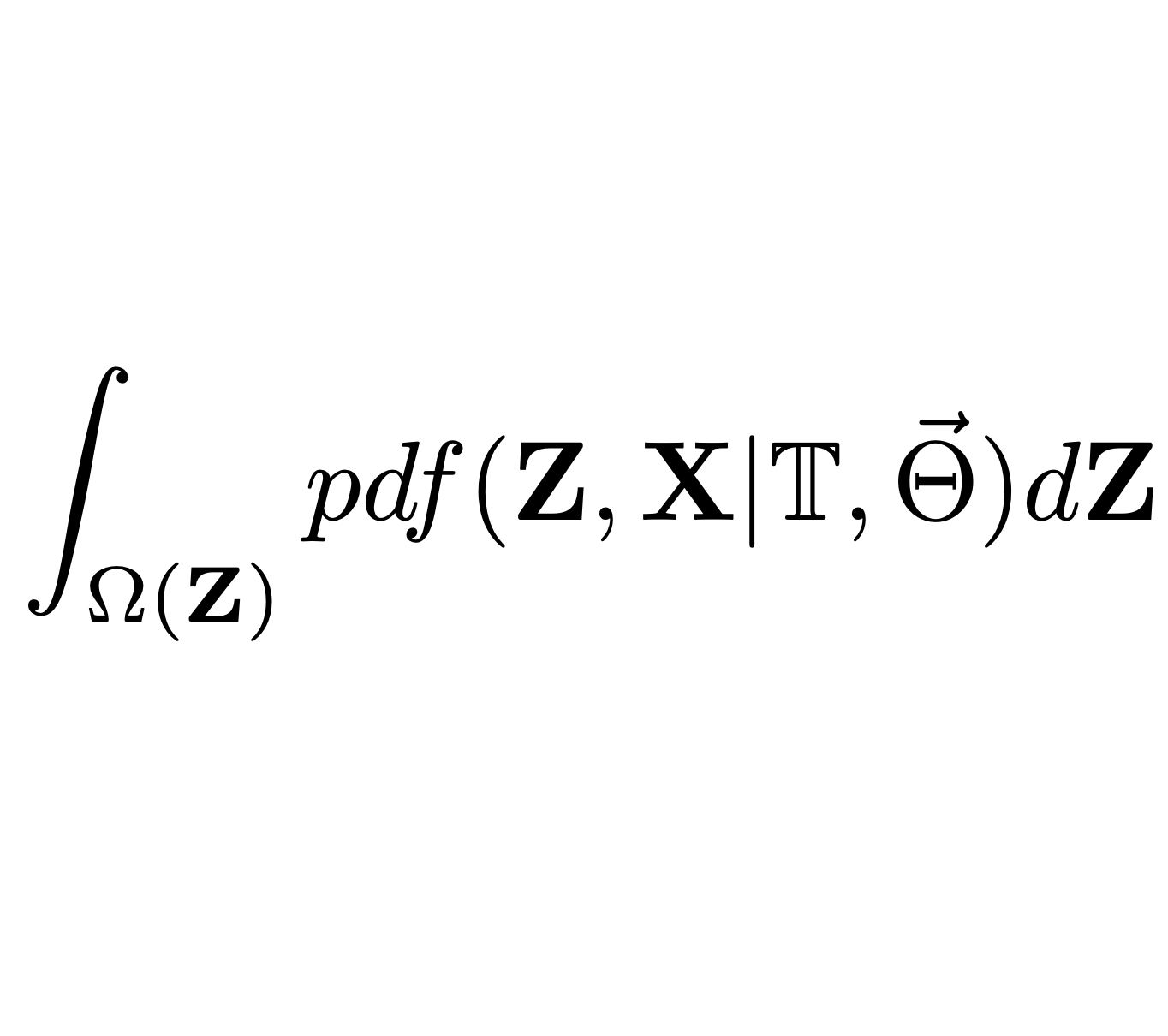Abstract

Phylogenetic comparative methods (PCMs) have been used to study the evolution of quantitative traits in various groups of organisms, ranging from micro-organisms to animal and plant species. A common approach has been to assume a Gaussian phylogenetic model for the trait evolution along the tree, such as a branching Brownian motion (BM) or an Ornstein–Uhlenbeck (OU) process. Then, the parameters of the process have been inferred based on a given tree and trait data for the sampled species. At the heart of this inference lie multiple calculations of the model likelihood, that is, the probability density of the observed trait data, conditional on the model parameters and the tree. With the increasing availability of big phylogenetic trees, spanning hundreds to several thousand sampled species, this approach is facing a two-fold challenge. First, the assumption of a single Gaussian process governing the entire tree is not adequate in the presence of heterogeneous evolutionary forces acting in different parts of the tree. Second, big trees present a computational challenge, due to the time and memory complexity of the model likelihood calculation.

Here, we explore a sub-family, denoted $G_{LInv}$, of the Gaussian phylogenetic models, with the transition density exhibiting the properties that the expectation depends Linearly on the ancestral trait value and the variance is Invariant with respect to the ancestral value. We show that $G_{LInv}$ contains the vast majority of Gaussian models currently used in PCMs, while supporting an efficient (linear in the number of nodes) algorithm for the likelihood calculation. The algorithm supports scenarios with missing data, as well as different types of trees, including trees with polytomies and non-ultrametric trees. To account for the heterogeneity in the evolutionary forces, the algorithm supports models with “shifts” occurring at specific points in the tree. Such shifts can include changes in some or all parameters, as well as the type of the model, provided that the model remains within the $G_{LInv}$ family. This contrasts with most of the current implementations where, due to slow likelihood calculation, the shifts are restricted to specific parameters in a single type of model, such as the long-term selection optima of an OU process, assuming that all of its other parameters, such as evolutionary rate and selection strength, are global for the entire tree.

We provide an implementation of this likelihood calculation algorithm in an accompanying R-package called PCMBase. The package has been designed as a generic library that can be integrated with existing or novel maximum likelihood or Bayesian inference tools.